Additively indecomposable ordinal

In set theory, a branch of mathematics, an additively indecomposable ordinal α is any ordinal number that is not 0 such that for any 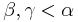$\beta,\gamma<\alpha$ , we have 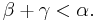$\beta%2B\gamma<\alpha.$ The set of additively indecomposable ordinals is denoted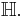 $\mathbb{H}.$

From the continuity of addition in its right argument, we get that if 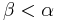$\beta < \alpha$ and α is additively indecomposable, then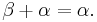 $\beta %2B \alpha = \alpha.$

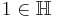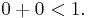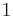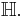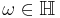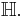
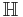Obviously $1\in\mathbb{H}$ , since $0%2B0<1.$ No finite ordinal other than $1$ is in $\mathbb{H}.$ Also, $\omega\in\mathbb{H}$ , since the sum of two finite ordinals is still finite. More generally, every infinite cardinal is in $\mathbb{H}.$

$\mathbb{H}$ is closed and unbounded, so the enumerating function of 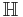$\mathbb{H}$ is normal. In fact,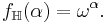 $f_\mathbb{H}(\alpha)=\omega^\alpha.$

The derivative 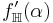$f_\mathbb{H}^\prime(\alpha)$ (which enumerates fixed points of f_H) is written 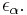$\epsilon_\alpha.$ Ordinals of this form (that is, fixed points of 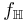$f_\mathbb{H}$ ) are called epsilon numbers. The number 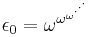$\epsilon_0=\omega^{\omega^{\omega^{\cdot^{\cdot^\cdot}}}}$ is therefore the first fixed point of the sequence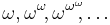 $\omega,\omega^\omega\!,\omega^{\omega^\omega}\!\!,\ldots$

Multiplicatively indecomposable

A similar notion can be defined for multiplication. The multiplicatively indecomposable ordinals are those of the form 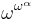$\omega^{\omega^\alpha} \,$ for any ordinal α.

Additively indecomposable ordinal

Multiplicatively indecomposable

See also